挑战 2022 年高考全国乙卷数学压轴大题

2022 年高考已落下帷幕，不少考生表示今年的数学是“历史第二难”。于是，我打算尝试一下今年全国乙卷数学的最后两道大题，切身体会一下今年学子们的不易。

解析几何

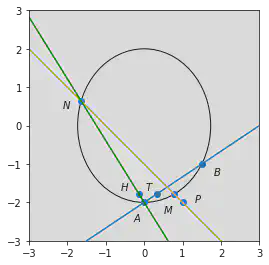
已知椭圆 $E$ 的中心为坐标原点，对称轴为 $x$ 轴、$y$ 轴，且过 $A(0,-2),B(\frac{3}{2},-1)$ 两点。

$(1)$ 求 $E$ 的方程；

$(2)$ 设过点 $P(1,-2)$ 的直线交 $E$ 于 $M,N$ 两点，过 $M$ 且平行于 $x$ 轴的直线与线段 $AB$ 交于点 $T$，点 $H$ 满足 $\vec{MT} = \vec{TH}$。证明：直线 $HN$ 过定点。

解：

设椭圆 $E$ 的方程为

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (a,b>0) $$

将 $A(0,-2),B(\frac{3}{2},-1)$ 两点坐标代入得

$$ \left\{\begin{align*} & \frac{4}{b^2} = 1 \\ & \frac{9}{4a^2} + \frac{1}{b^2} = 1 \end{align*}\right. $$

解得

$$ \left\{\begin{align*} \ & a^2 = 3 \\ \ & b^2 = 4 \end{align*}\right. $$

因此椭圆 $E$ 的方程为

$$ \frac{x^2}{3} + \frac{y^2}{4} = 1 $$

第 $(2)$ 小题给出的条件特别多，我们慢慢梳理这些条件。首先条件中提到了线段 $AB$，并且有一条直线与线段 $AB$ 有交点。因此需要给出直线 $AB$ 的方程，用两点式表示，得到

$$ \begin{align*} \frac{y + 2}{x} &= \frac{2}{3} \end{align*} $$

化为一般式

$$ l_{AB}: 2x - 3y - 6 = 0 $$

由于本题是证明题，我们可以通过特例得出答案，然后再证明其一般性。因此，我们考察过 $P$ 点的竖直直线这一情况。此时 $M$ 点的横坐标为 $1$，代入椭圆方程得到

$$ \frac{1}{3} + \frac{y^2}{4} = 1 $$

解得

$$ y = \pm \frac{2\sqrt{6}}{3} $$

即 $M,N$ 两点的坐标分别为 $(1,-\frac{2\sqrt{6}}{3}),(1,\frac{2\sqrt{6}}{3})$。于是将 $y=-\frac{2\sqrt{6}}{3}$ 代入直线 $AB$ 的方程

$$ 2x + 2\sqrt{6} - 6 = 0 $$

解得

$$ x = 3 - \sqrt{6} $$

即 $T$ 点的坐标为 $(3-\sqrt{6},-\frac{2\sqrt{6}}{3})$。依题意，$\vec{MT} = \vec{TH}$，我们可以求出 $\vec{MT}$ 的坐标：

$$ \vec{MT} = (2-\sqrt{6},0) $$

于是 $H$ 点的坐标为 $(5-2\sqrt{6}, -\frac{2\sqrt{6}}{3})$。下面就可以利用两点式写出直线 $HN$ 的方程：

$$ \frac{y - \frac{2\sqrt{6}}{3}}{x - 1} = \frac{-\frac{2\sqrt{6}}{3} - \frac{2\sqrt{6}}{3}}{4-2\sqrt{6}} $$

整理之后得到

$$ y = (2 - \frac{2\sqrt{6}}{3})x - 2 $$

可以看出，直线 $HN$ 过点 $(0,-2)$。那么是不是一定过定点 $(0,-2)$ 呢？目前得出的结论是无法判断的，但我们可以猜想直线 $HN$ 过定点 $(0,-2)$。为了证明这个猜想，我们还需要进行不失一般性的计算。

过点 $P(1,-2)$ 的直线与椭圆 $E$ 相交与 $M,N$ 两点，我们设其点斜式方程为：

$$ l_{MN}: y + 2 = k(x - 1) $$

将其与椭圆 $E$ 的方程联立，并代入得

$$ \begin{align*} 4x^2 + 3[k^2(x-1)^2 - 4k(x-1) + 4] - 12 &= 0 \\ (3k^2+4)x^2 - 6k(k + 2)x + 3k(k+4) &= 0 \end{align*} $$

设 $M,N$ 两点坐标分别为 $(x_1,y_1),(x_2,y_2)$，由韦达定理得

$$ \begin{align*} x_1+x_2 &= \frac{6k(k+2)}{3k^2+4} \tag{1} \\ x_1x_2 &= \frac{3k(k+4)}{3k^2+4} \tag{2} \end{align*} $$

进一步可以得到

$$ \begin{align*} y_1+y_2 &= k(x_1+x_2) - 2k - 4 \\ &= \frac{6k^2(k+2)}{3k^2+4} - \frac{(2k+4)(3k^2+4)}{3k^2+4} \\ &= -\frac{8(k+2)}{3k^2+4} \tag{3} \end{align*} $$ $$ \begin{align*} y_1y_2 &= [k(x_1-1) - 2][k(x_2-1) - 2] \\ &= k^2(x_1x_2 - x_1 - x_2 + 1) - 2k(x_1 - 1) - 2k(x_2 - 1) + 4 \\ &= k^2x_1x_2 - k(k+2)(x_1+x_2) + (k+2)^2 \\ &= \frac{3k^3(k+4)}{3k^2+4} - \frac{6k^2(k+2)^2}{3k^2+4} + \frac{(k+2)^2(3k^2+4)}{3k^2+4} \\ &= -\frac{8(k^2 - 2k - 2)}{3k^2+4} \tag{4} \\ \end{align*} $$ $$ \begin{align*} x_1y_2 + x_2y_1 &= x_1(kx_2 - k - 2) + x_2(kx_1 - k - 2) \\ &= 2kx_1x_2 - (k+2)(x_1+x_2) \\ &= \frac{6k^2(k+4)}{3k^2+4} - \frac{6k(k+2)^2}{3k^2+4} \\ &= -\frac{24k}{3k^2+4} \tag{5} \end{align*} $$

式 $(1)$-$(5)$ 是下面计算化简的依据，我们在这里提前准备好。

依题意，过 $M$ 且平行于 $x$ 的直线交线段 $AB$ 于点 $T$。我们将 $y=y_1$ 代入直线 $AB$ 的方程，得到

$$ \begin{align*} 2x - 3y_1 - 6 &= 0 \\ x &= \frac{3}{2}y_1+3 \end{align*} $$

于是可以得到 $T$ 点的坐标为

$$ (\frac{3}{2}y_1+3, y_1) $$

依题意，$\vec{MT} = \vec{TH}$，说明 $T$ 是线段 $HM$ 的中点。并且线段 $HM$ 显然与 $x$ 轴平行，$H$ 点的纵坐标与 $T$ 点相同，横坐标可以用如下的中点坐标公式求得

$$ \begin{align*} x_H &= 2 \times (\frac{3}{2}y_1+3) - x_1 \\ &= 3y_1 - x_1 + 6 \end{align*} $$

于是可以得到 $H$ 点的坐标为

$$ (3y_1 - x_1 + 6, y_1) $$

现在，可以用两点式写出直线 $HN$ 的方程

$$ \begin{align*} l_{HN}: \frac{y - y_2}{x - x_2} &= \frac{y_1 - y_2}{3y_1 - x_1 + 6 - x_2} \end{align*} $$

化简以后得到

$$ \begin{align*} (y_1-y_2)x - (3y_1-x_1-x_2+6)y + 3y_1y_2 + 6y_2 - x_1y_2 - x_2y_1 &= 0 \end{align*} $$

我们仔细观察上式，发现有很多项已经在我们之前利用韦达定理以及由其导出的结果中出现，例如 $y_1y_2$、$x_1y_2 + x_2y_1$。但是还有个别的 $y_1$、$y_2$ 之前的系数待定，甚至还出现了 $y_1-y_2$。很巧妙的一点是，我们将点 $(0, -2)$ 代入得

$$ \begin{align*} 6(y_1+y_2) - 2(x_1+x_2) + 12 + 3y_1y_2 - x_1y_2 - x_2y_1 &= 0 \\ \end{align*} $$

发现所有那些无法配对的项都可以成功配对了！我们尝试将所有的 $x_1,x_2,y_1,y_2$ 都用 $k$ 来表示，得到

$$ \begin{align*} 6(y_1+y_2) - 2(x_1+x_2) + 12 + 3y_1y_2 - x_1y_2 - x_2y_1 &= 0 \\ -\frac{48(k+2)}{3k^2+4} - \frac{12k(k+2)}{3k^2+4} + 12 - \frac{24(k^2 - 2k - 2)}{3k^2+4} + \frac{24k}{3k^2+4} &= 0 \\ 48(k+2) + 12k(k+2) + 24(k^2-2k-2) - 24k &= 12(3k^2 + 4) \\ 36k^2 + 48 &= 12(3k^2 + 4) \end{align*} $$

可以看到上述等式恒成立，与 $k$ 的取值无关。

综上所述，直线 $HN$ 过定点 $(0,-2)$。

点评

本题题型较为常规，是一个证明直线过定点的问题。证明直线过定点的问题一般有如下两种思路：

1. 直接整理出带参数的直线点斜式方程，然后直接看出直线所过定点。
2. 首先通过特例判断定点坐标，然后再加以不失一般性的证明。

然而，本题的条件特别多，这需要我们认真捋顺各点的关系。直线 $MN$ 的过定点 $P$，$MN$ 倾斜角的变化带动 $M,N$ 两点坐标的变化。后又出现 $T,H$ 两点，且和 $M$ 点满足一定的数量关系。最后又将 $H,N$ 两点连接起来。

我们经过一步步的推导，将直线 $HN$ 的方程最终表示为与 $M,N$ 两点相关的带参数的方程。但是，这个时候并不能将所有参数用某一个参数表示，因此通过因式分解等方法化简直线方程以看出直线过定点的方法行不通。

但本题是证明题，我们就可以先通过特例尝试猜想直线 $HN$ 过哪个定点。特例的选取应当具有一定的特殊性，并且计算简便。平行于坐标轴的直线由于其方程仅含 $x$ 或 $y$ 而计算简便，根据本题的具体情况，我们选择和 $y$ 轴平行的竖直直线，并且很容易地得到了它的方程。

我们之所以可以猜想直线 $HN$ 过定点 $(0,-2)$，是因为

$$ \left\{\begin{align*} \ & x = 0 \\ \ & y = -2 \end{align*}\right. $$

是二元一次方程

$$ y = (2 - \frac{2\sqrt{6}}{3})x - 2 $$

唯一的一对有理数解。从 $x$ 前的系数是无理数就可以看出来这一性质。如果直线 $HN$ 所经过定点的坐标包含无理数，那么不失一般性的计算必然无法化简。换而言之，我们也只有尝试 $(0,-2)$ 这一点的可能。结果，经过我们的证明，直线 $HN$ 确实过定点 $(0,-2)$。

本题巧妙之处就在于，我们所选择的特例仅过 $(0,-2)$ 唯一一个有理数点，这为我们判断直线 $HN$ 过定点 $(0,-2)$ 带来了极大的方便。如果特例的方程不含无理数，我们仍然难以判断直线 $HN$ 究竟过哪个定点。

不过，本题的难点在于计算量较大。除了韦达定理本身以外，还需要导出一些其他的结果以便于将所有点的坐标用 $k$ 表示。此外，还需要对式子有敏锐的观察力，每项如何凑在一起可以“消灭”。如果不能够冷静观察式子的结构，在考场上很难有信心继续算下去。

函数与导数

已知函数 $f(x) = \ln (1+x) + axe^{-x}$。

$(1)$ 当 $a = 1$ 时，求曲线 $y = f(x)$ 在点 $(0,f(0))$ 处的切线方程；

$(2)$ 若 $f(x)$ 在区间 $(-1,0),(0,+\infty)$ 各恰有一个零点，求 $a$ 的取值范围。

解：

依题意，当 $a=1$ 时，

$$ f(x) = \ln (1+x) + xe^{-x} $$

第 $(1)$ 小题要求切线方程，因此需要利用导数。我们对 $f(x)$ 求导得

$$ f^{\prime}(x) = \frac{1}{1 + x} + (1-x) e^{-x} $$

于是点 $(0,f(0))$ 处的切线斜率为

$$ f^{\prime}(0) = 2 $$

故点 $(0,f(0))$ 处的切线方程为

$$ y = 2x $$

要回答第 $(2)$ 小题，我们需要直接对 $f(x)$ 求导，得到

$$ \begin{align*} f^{\prime}(x) &= \frac{1}{1 + x} + a(1-x) e^{-x} \\ &= \frac{1 + a(1-x^2)e^{-x}}{1+x} \end{align*} $$

这个式子很难判断零点和单调性。但考虑到函数 $f(x)$ 的定义域为 $(-1,+\infty)$，因此分母恒正。下面我们单独来处理导函数的分子，令

$$ g(x) = 1 + a(1-x^2)e^{-x} $$

对 $g(x)$ 求导，得到

$$ \begin{align*} g^{\prime}(x) &= a[-2xe^{-x} + (x^2-1)e^{-x}] \\ &= a(x^2 - 2x - 1)e^{-x} \end{align*} $$

于是，我们令 $g^{\prime}(x)=0$，可以解得两根

$$ \left\{\begin{align*} \ & x_1 = 1 - \sqrt{2} \\ \ & x_2 = 1 + \sqrt{2} \end{align*}\right. $$

由于 $e^{-x}>0$ 恒成立，$g^{\prime}(x)$ 的正负就取决于 $a$ 的正负了。因此，我们按照如下情况进行分类讨论：

1. $a=0$

若 $a=0$，则 $g^{\prime}(x)=0$ 恒成立，$g(x) \equiv 1$。于是 $f^{\prime}(x) > 0$ 恒成立，这说明 $f(x)$ 在整个定义域 $(-1,+\infty)$ 上单调递增。这无论如何都不符合题意，因为 $f(x)$ 至多只可能有一个零点。

2. $a>0$

若 $a>0$，则 $g^{\prime}(x)$ 的正负性以及 $g(x)$ 的单调性如下表：

区间	$g^{\prime}(x)$	$g(x)$
$(-1,1-\sqrt{2})$	$+$	$\nearrow$
$(1-\sqrt{2},1+\sqrt{2})$	$-$	$\searrow$
$(1+\sqrt{2},+\infty)$	$+$	$\nearrow$

下面，我们分别计算驻点和一些关键点的函数值，并判断它们的正负。

$$ \begin{align*} g(-1) &= 1 > 0 \\ g(1-\sqrt{2}) &= 1 + \sqrt{2}a(2-\sqrt{2})e^{\sqrt{2}-1} > 0 \\ g(0) &= a + 1 > 0 \\ g(1) &= 1 > 0 \\ g(1+\sqrt{2}) &= 1 - \sqrt{2}a(2+\sqrt{2})e^{-(\sqrt{2}+1)} \\ \end{align*} $$

由于 $-1$ 不在 $f^{\prime}(x)$ 的定义域内，不过我们可以根据 $g(x)$ 的正负以及单调性判断 $f^{\prime}(x)>0$ 在 $(-1,0)$ 上恒成立，当然也可以利用下列极限来判断：

$$ \lim_{x\rightarrow-1^+} f^{\prime}(x) = \lim_{x\rightarrow-1^+}[\frac{1}{1 + x} + a(1-x) e^{-x}] = +\infty $$

因此 $f(x)$ 在 $(-1,0)$ 上单调递增。不过，根据对数函数的性质，我们可以判断下列极限

$$ \lim_{x\rightarrow-1^+} f(x) = \lim_{x\rightarrow-1^+} [\ln (1+x) + axe^{-x}] = -\infty $$

而 $f(0)=0$。因此可以判断，$f(x)<0$ 在 $(-1,0)$ 上恒成立，这并不符合题意中的 $(-1,0)$ 内恰有一个零点。

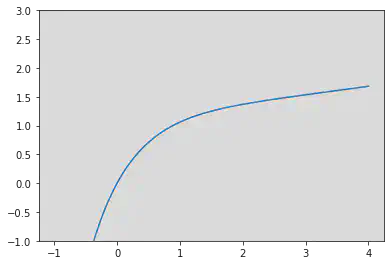
下图是 $a=1$ 时函数 $f(x)$ 的图像，可以帮助我们理解。

3. $a<0$

若 $a<0$，则 $g^{\prime}(x)$ 的正负性以及 $g(x)$ 的单调性如下表：

区间	$g^{\prime}(x)$	$g(x)$
$(-1,1-\sqrt{2})$	$-$	$\searrow$
$(1-\sqrt{2},1+\sqrt{2})$	$+$	$\nearrow$
$(1+\sqrt{2},+\infty)$	$-$	$\searrow$

同样地，我们还是分别计算驻点和一些关键点的函数值，并判断它们的正负。

$$ \begin{align*} g(-1) &= 1 > 0 \\ g(1-\sqrt{2}) &= 1 + \sqrt{2}a(2-\sqrt{2})e^{\sqrt{2}-1} \\ g(0) &= a + 1 \\ g(1) &= 1 > 0 \\ g(1+\sqrt{2}) &= 1 - \sqrt{2}a(2+\sqrt{2})e^{-(\sqrt{2}+1)} > 0 \\ \end{align*} $$

可以看到，当 $a<0$ 时，情况有些变化，我们无法判断 $g(1-\sqrt{2})$ 和 $g(0)$ 的正负性。不过，$g(0)$ 是一个关于 $a$ 的函数，并且表达式简单，我们可以再分情况讨论 $g(0)$ 的正负性。

① $a = -1$

此时 $g(0)=0$，$f^{\prime}(0)=0$，而 $g(x)$ 在 $(1-\sqrt{2},1+\sqrt{2})$ 上单调递增，$f^{\prime}(x)$ 也有着和 $g(x)$ 同样的增减性。虽然 $g(x)$ 在 $(1+\sqrt{2},+\infty)$ 上单调递减，但下列极限

$$ \lim_{x\rightarrow+\infty} g(x) = \lim_{x\rightarrow+\infty} (1 + \frac{x^2-1}{e^x}) = 1 > 0 $$

因此，可以判断 $g(x)>0$ 在 $(0,+\infty)$ 上恒成立，即 $f^{\prime}(x)>0$ 在 $(0,+\infty)$ 上恒成立。因此，$f(x)$ 在 $(0,+\infty)$ 上单调递增，$f(x)>f(0)=0$。这样也并不符合题意。

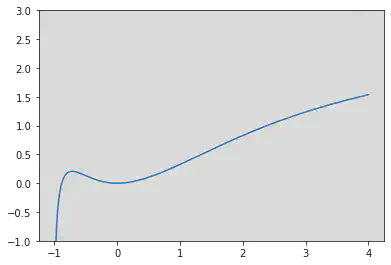
下图是 $a=-1$ 时函数 $f(x)$ 的图像。可以看到，函数 $f(x)$ 的图像正好与 $x$ 轴相切于原点。

② $-1<a<0$

和情况 ① 类似，此时 $g(0)>0$，$f^{\prime}(0) = a+1 > 0$。通过判断极限 $\lim_{x\rightarrow+\infty} g(x) > 0$，可以证明 $g(x)>0$ 在 $(0,+\infty)$ 上恒成立，即 $f^{\prime}(x)>0$ 在 $(0,+\infty)$ 上恒成立。因此，$f(x)$ 在 $(0,+\infty)$ 上单调递增，$f(x)>f(0)=0$。这同样也并不符合题意。

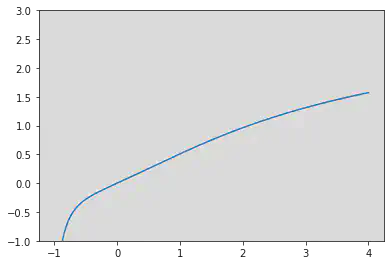
下图是 $a=-\frac{1}{2}$ 时函数 $f(x)$ 的图像，和 $a>0$ 的情况类似。

③ $a<-1$

和情况 ①、② 都不同，此时 $g(0)<0$，$f^{\prime}(0) = a+1 < 0$。又因为 $g(-1)>0$，且 $g(x)$ 在 $(-1,1-\sqrt{2})$ 上单调递减，在 $(1-\sqrt{2},0)$ 上单调递增。这样，虽然我们一开始不好判断 $g(1-\sqrt{2})$ 的正负性，但是我们凭借 $g(x)$ 的单调性以及 $g(0)<0$，我们就可以判断 $g(1-\sqrt{2})<0$。因此 $\exists! m \in (-1,1-\sqrt{2})$，使得 $g(m)=f^{\prime}(m)=0$，即

$$ \begin{align*} 1 + a(1-m^2)e^{-m} &= 0 \\ ae^{-m} &= \frac{1}{m^2-1} \end{align*} $$

同理，$g(1)>0$，且 $g(x)$ 在 $(1-\sqrt{2},1+\sqrt{2})$ 上单调递增。因此 $\exists! n \in (0,1)$，使得 $g(n) = f^{\prime}(n) = 0$，即

$$ \begin{align*} 1 + a(1-n^2)e^{-n} &= 0 \\ ae^{-n} &= \frac{1}{n^2-1} \end{align*} $$

综合以上，我们可以得出 $f^{\prime}(x)$ 的正负性和 $f(x)$ 的增减性，如下表所示：

区间	$f^{\prime}(x)$	$f(x)$
$(-1,m)$	$+$	$\nearrow$
$(m,n)$	$-$	$\searrow$
$(n,+\infty)$	$+$	$\nearrow$

有了 $f(x)$ 的增减性，我们就容易判断 $f(x)$ 的零点分布了。首先计算并且判断 $f(m)$、$f(n)$ 的大小：

$$ \begin{align*} f(m) &= \ln (1+m) + ame^{-m} \\ &= \ln (1+m) + \frac{m}{m^2-1} \\ f(n) &= \ln (1+n) + ane^{-n} \\ &= \ln (1+n) + \frac{n}{n^2-1} \end{align*} $$

不过，$f(m)$、$f(n)$ 的大小难以判断，需要借助导数来帮助判断。令

$$ h(x) = \ln (1+x) + \frac{x}{x^2-1} $$

对 $h(x)$ 求导，有

$$ \begin{align*} h^{\prime}(x) &= \frac{1}{1+x} + \frac{x^2-1 - 2x^2}{(x^2-1)^2} \\ &= \frac{(x+1)(x-1)^2 - x^2 - 1}{(x+1)^2(x-1)^2} \\ &= \frac{x[(x-1)^2-2]}{(x+1)^2(x-1)^2} \end{align*} $$

分子虽然是三次多项式，但可以根据“穿根引线”法来判断 $h^{\prime}(x)$ 的零点和以及 $h(x)$ 单调性。显然，$h^{\prime}(x)$ 有三个零点：$1-\sqrt{2},0,1+\sqrt{2}$。不过要特别注意的一点是，$h^{\prime}(x)$ 有无穷间断点 $x=1$。于是，我们总结函数 $h^{\prime}(x)$ 的正负性和 $h(x)$ 的单调性如下表所示。

区间	$h^{\prime}(x)$	$h(x)$
$(-1,1-\sqrt{2})$	$-$	$\searrow$
$(1-\sqrt{2},0)$	$+$	$\nearrow$
$(0,1)$	$-$	$\searrow$
$(1,1+\sqrt{2})$	$-$	$\searrow$
$(1+\sqrt{2},+\infty)$	$+$	$\nearrow$

$h(x)$ 的图像如下图所示：

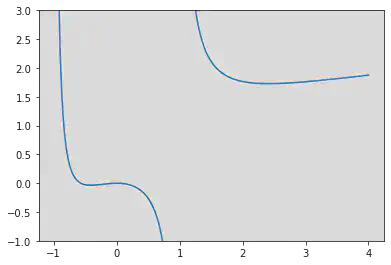
我们可以很容易得到 $h(0)=0$。并且我们观察到，$h(1)<0$，且 $h(x)$ 在 $(0,1)$ 上单调递减。因此我们可以判断 $f(n)<0$。又 $m \in (-1,1-\sqrt{2})$，$f(0)=0$，且 $f(x)$ 在 $(m,n)$ 上单调递减。这样我们又可以判断 $f(m)>0$。

现在所有的结论都已经推导出来了，下面先说明零点的存在性。

$$ \begin{align*} \lim_{x \rightarrow -1^+} f(x) &= \lim_{x \rightarrow -1^+} [\ln (1+x) + axe^{-x}] = -\infty < 0 \\ f(m) &> 0 \end{align*} $$

并且函数 $f(x)$ 连续。因此，$\exists x_1 \in (-1,m)$，使得 $f(x_1)=0$。同理可得

$$ \begin{align*} f(n) &< 0 \\ \lim_{x \rightarrow +\infty} f(x) &= \lim_{x \rightarrow +\infty} [\ln (1+x) + axe^{-x}] = +\infty > 0 \\ \end{align*} $$

并且函数 $f(x)$ 连续。因此，$\exists x_2 \in (n,+\infty)$，使得 $f(x_2)=0$。存在性得证。

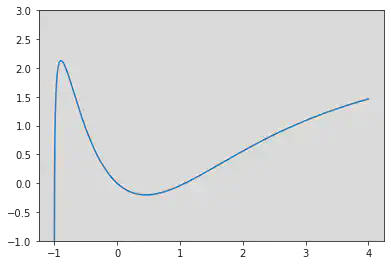
下面说明零点的唯一性。首先，$f(0)=0$，$f(x)$ 在 $(m,n)$ 上单调递减。又因为 $f(m)>0$ 且 $f(n)<0$，所以 $f(x)>0$ 在 $(m,0)$ 上恒成立，$f(x)<0$ 在 $(0,n)$ 上恒成立。而 $f(x)$ 分别在 $(-1,m)$ 和 $(n,+\infty)$ 上都是单调的，因此刚才所证明存在的零点分别是 $(-1,0)$ 和 $(0,+\infty)$ 上的唯一零点。具体可以参考下图理解：

点评

本题题型较为常规，是一个判断函数零点的问题。不过，本题的难度较大。一方面，本题的参数 $a$ 需要分类讨论；另一方面，题目中并没有给出不等式的条件，也没有某个其他函数，使得我们可以通过放缩法与之建立不等关系，这样我们想要通过参变分离的方法转化为求值域问题的思路就不再可行。

本题对参数 $a$ 的讨论是分为两个层次的。首先，我们对 $a$ 与 $0$ 的大小关系进行讨论。这是因为一阶导数的分子 $g(x)$ 的正负与 $a$ 的正负相关，它会影响到 $f(x)$ 的单调性。

其次，当 $a<0$ 时，$g(0)$ 的大小，即 $a+1$ 的正负，对 $g(x)$ 的正负会有很大影响，也会影响到 $f(x)$ 的单调性。所以我们又对 $a$ 和 $-1$ 的关系进行了讨论。不过，我们很容易就判断出 $-1 \leqslant a < 0$ 的情况不合题意，因此只有 $a<-1$ 有进一步讨论的空间。

接下来，我们判断出 $f(x)$ 的单调区间，并且是带有参数的，这使得我们难以判断驻点的正负。为此，我们将零点的条件代入 $f(x)$，以消去参数 $a$，并且构造一个新的函数研究其性质。经过研究，我们终于判断出了 $f(x)$ 两个驻点的正负，并且证明两个开区间上零点的存在性和唯一性。

虽然本题题型较为常规，但本题在零点问题中是非常难的。它不光考察了考生零点定理的理解和运用，还考察了函数与导数关系的熟练运用，以及分类讨论的思想。