挑战 2023 年高考全国乙卷数学压轴大题
2023 年高考已落下帷幕,不少考生反映今年的试题相较过去几年要容易一些。按照惯例,我继续尝试一下今年全国乙卷数学的最后两道大题。
解析几何
- 已知曲线 $C$ 的方程为 $\frac{y^2}{a^2}+\frac{x^2}{b^2}=1 (a>b>0)$,离心率为 $\frac{\sqrt{5}}{3}$,曲线过点 $A(-2,0)$。
(1) 求曲线 $C$ 的方程。
(2) 过点 $(-2,3)$ 的直线交曲线 $C$ 于 $P,Q$ 两点,直线 $AP,AQ$ 与 $y$ 轴交于 $M,N$ 两点。证明:线段 $MN$ 的中点是定点。
解:
(1)
将点 $(-2,0)$ 代入曲线 $C$ 的方程,得到
$$ \frac{4}{b^2} = 1 $$解得 $b=2$(负值舍去)。
根据离心率的定义,可以列出如下方程
$$ \frac{a^2-b^2}{a^2} = (\frac{\sqrt{5}}{3})^2 $$将 $b=2$ 代入,解得 $a=3$(负值舍去)。
因此曲线 $C$ 的方程为
$$ \frac{y^2}{9}+\frac{x^2}{4}=1 $$(2)
设直线 $PQ$ 的方程为
$$ l_{PQ}: y-3 = k(x+2) $$将之与曲线 $C$ 的方程联立
$$ \begin{cases} 4y^2+9x^2-36=0 \\ y = kx+(2k+3) \end{cases} $$消去 $y$ 得到
$$ (4k^2+9)x^2 + 8k(2k+3)x + 16k(k+3) = 0 $$设 $P,Q$ 两点的坐标分别为 $(x_1,y_1),(x_2,y_2)$,由韦达定理得
$$ \begin{aligned} x_1+x_2 &= -\frac{8k(2k+3)}{4k^2+9} \\ x_1x_2 &= \frac{16k(k+3)}{4k^2+9} \end{aligned} $$直线 $AP,AQ$ 的方程分别为
$$ \begin{aligned} l_{AP}: \frac{y}{x+2} = \frac{y_1}{x_1+2} \\ l_{AQ}: \frac{y}{x+2} = \frac{y_2}{x_2+2} \end{aligned} $$分别令其中的 $x=0$,可以得到 $M,N$ 两点的坐标
$$ \begin{aligned} M(0, \frac{2y_1}{x_1+2}) \\ N(0, \frac{2y_2}{x_2+2}) \end{aligned} $$线段 $MN$ 的中点坐标为
$$ (0, \frac{y_1}{x_1+2}+\frac{y_2}{x_2+2}) $$下面计算线段 $MN$ 中点的纵坐标
$$ \begin{aligned} & \frac{y_1}{x_1+2}+\frac{y_2}{x_2+2} \\ =& \frac{x_1y_2+x_2y_1 + 2(y_1+y_2)}{x_1x_2 + 2(x_1+x_2) + 4} \\ =& \frac{2kx_1x_2 + (4k+3)(x_1+x_2) + 4(2k+3)}{x_1x_2 + 2(x_1+x_2) + 4} \\ =& \frac{\frac{32k^2(k+3)}{4k^2+9}-\frac{8k(4k+3)(2k+3)}{4k^2+9}+4(2k+3)}{\frac{16k(k+3)}{4k^2+9}-\frac{16k(2k+3)}{4k^2+9}+4} \\ =& \frac{32k^2(k+3) - 8k(4k+3)(2k+3) + 4(2k+3)(4k^2+9)}{16k(k+3) - 16k(2k+3) + 4(4k^2+9)} \\ =& \frac{32k^2(k+3) + (2k+3)(-16k^2-24k+36)}{36} \\ =& 3 \end{aligned} $$即证明线段 $MN$ 的中点是定点 $(0,3)$。
可视化

from manim import *
class MyEllipse(MovingCameraScene):
def __init__(self):
super().__init__()
self.plane = NumberPlane(x_range=[-20, 20], y_range=[-20, 20])
# self.ellipse = Ellipse(2, 3).scale(2).set_color(WHITE)
self.ellipse = ParametricFunction(lambda t: np.array([2 * np.cos(t), 3 * np.sin(t), 0]), t_range=[0, 2 * PI])
self.dot = Dot([-2, 3, 0]).set_color(RED)
self.dot_label = MathTex(r"(-2,3)").scale(0.8).next_to(self.dot, UP)
self.a = Dot([-2, 0, 0]).set_color(RED) # A 点
self.a_label = MathTex(r"A").scale(0.8).next_to(self.a, LEFT + DOWN)
self.tracker = ValueTracker(-5) # 斜率
self.k_label = MathTex(r"k = -5").to_corner(RIGHT + UP)
self.k_label.add_updater(
lambda x: x.become(MathTex(r"k = %.2f" % self.tracker.get_value()).to_corner(RIGHT + UP)))
# 直线 PQ
self.pq = Line(self.dot, [2, 4 * self.tracker.get_value() + 3, 0]).set_color(RED)
self.pq.add_updater(
lambda x: x.put_start_and_end_on([self.dot.get_x(), self.dot.get_y(), self.dot.get_z()],
[2, 4 * self.tracker.get_value() + 3, 0]))
# P 点
self.p = Dot(self.get_p_pos()).set_color(GREEN)
self.p.add_updater(lambda x: x.move_to(self.get_p_pos()))
self.p_label = MathTex(r"P").scale(0.8).next_to(self.p, LEFT)
self.p_label.add_updater(lambda x: x.next_to(self.p, LEFT))
# Q 点
self.q = Dot(self.get_q_pos()).set_color(GREEN)
self.q.add_updater(lambda x: x.move_to(self.get_q_pos()))
self.q_label = MathTex(r"Q").scale(0.8).next_to(self.q, RIGHT)
self.q_label.add_updater(lambda x: x.next_to(self.q, RIGHT))
# 线段 AP
self.ap = Line(self.a, self.p).set_color(YELLOW)
self.ap.add_updater(lambda x: x.put_start_and_end_on([self.a.get_x(), self.a.get_y(), self.a.get_z()],
[self.p.get_x(), self.p.get_y(), self.p.get_z()]))
# 线段 AQ
self.aq = Line(self.a, self.q).set_color(YELLOW)
self.aq.add_updater(lambda x: x.put_start_and_end_on([self.a.get_x(), self.a.get_y(), self.a.get_z()],
[self.q.get_x(), self.q.get_y(), self.q.get_z()]))
# M 点
self.m = Dot(self.get_m_pos()).set_color(PURPLE)
self.m.add_updater(lambda x: x.move_to(self.get_m_pos()))
self.m_label = MathTex(r"M").scale(0.8).next_to(self.m, LEFT + UP)
self.m_label.add_updater(lambda x: x.next_to(self.m, LEFT + UP))
# N 点
self.n = Dot(self.get_n_pos()).set_color(PURPLE)
self.n.add_updater(lambda x: x.move_to(self.get_n_pos()))
self.n_label = MathTex(r"N").scale(0.8).next_to(self.n, LEFT + DOWN)
self.n_label.add_updater(lambda x: x.next_to(self.n, RIGHT + DOWN))
# 线段 PM
self.pm = Line(self.p, self.m).set_color(YELLOW)
self.pm.add_updater(lambda x: x.put_start_and_end_on(
[self.p.get_x(), self.p.get_y(), self.p.get_z()],
[self.m.get_x(), self.m.get_y(), self.m.get_z()]
) if self.p.get_x() < 0 else x.move_to(Point([100, 100, 0])))
# 线段 QN
self.qn = Line(self.q, self.n).set_color(YELLOW)
self.qn.add_updater(lambda x: x.put_start_and_end_on(
[self.q.get_x(), self.q.get_y(), self.q.get_z()],
[self.n.get_x(), self.n.get_y(), self.n.get_z()]
) if self.q.get_x() < 0 else x.move_to(Point([100, 100, 0])))
# 线段 MN
self.mn = Line(self.m, self.n).set_color(BLUE)
self.mn.add_updater(lambda x: x.put_start_and_end_on([self.m.get_x(), self.m.get_y(), self.m.get_z()],
[self.n.get_x(), self.n.get_y(), self.n.get_z()]))
# MN 中点
self.mid = Dot(midpoint([self.m.get_x(), self.m.get_y(), self.m.get_z()],
[self.n.get_x(), self.n.get_y(), self.n.get_z()])).set_color(PINK)
self.mid.add_updater(lambda x: x.move_to(midpoint([self.m.get_x(), self.m.get_y(), self.m.get_z()],
[self.n.get_x(), self.n.get_y(), self.n.get_z()])))
def construct(self):
self.add(self.plane)
self.play(Create(self.ellipse))
self.wait()
self.play(Create(self.dot), Create(self.dot_label))
self.wait()
self.play(Create(self.pq))
self.wait()
self.play(Create(self.p), Create(self.p_label), Create(self.q), Create(self.q_label))
self.wait()
self.play(Create(self.a), Create(self.a_label))
self.wait()
self.play(Create(self.ap))
self.play(Create(self.aq))
self.wait()
self.play(self.camera.frame.animate.scale(1.5))
self.wait()
self.play(Create(self.pm), Create(self.m), Create(self.m_label))
self.play(Create(self.qn), Create(self.n), Create(self.n_label))
self.wait()
self.play(Create(self.mn))
self.play(Create(self.mid))
self.wait()
self.play(self.camera.frame.animate.move_to([0, 3, 0]))
self.wait()
self.play(Create(self.k_label))
self.wait()
self.play(self.tracker.animate.set_value(0), run_time=15, rate_func=rate_functions.smooth)
self.wait()
def get_p_pos(self):
k = self.tracker.get_value()
a = 4 * (k ** 2) + 9
b = 8 * k * (2 * k + 3)
c = 16 * k * (k + 3)
x_p, _ = MyEllipse.solve_quadratic_equation(a, b, c)
y_p = k * x_p + 2 * k + 3
return [x_p, y_p, 0]
def get_q_pos(self):
k = self.tracker.get_value()
a = 4 * (k ** 2) + 9
b = 8 * k * (2 * k + 3)
c = 16 * k * (k + 3)
_, x_q = MyEllipse.solve_quadratic_equation(a, b, c)
y_q = k * x_q + 2 * k + 3
return [x_q, y_q, 0]
def get_m_pos(self):
k = self.ap.get_slope()
y_m = 2 * k
return [0, y_m, 0]
def get_n_pos(self):
k = self.aq.get_slope()
y_n = 2 * k
return [0, y_n, 0]
@staticmethod
def solve_quadratic_equation(a, b, c):
import math
if a == 0:
if b == 0:
if c == 0:
# print("方程解为全体实数")
return None
else:
# print("方程无实数解")
return None
else:
x = -c / b
# print(f"方程为一次方程,解为 x={x}")
return x
else:
delta = b ** 2 - 4 * a * c
if delta < 0:
# print("方程无实数解")
return None
elif delta == 0:
x = -b / (2 * a)
# print(f"方程有唯一解,x={x}")
return x, x
else:
x1 = (-b - math.sqrt(delta)) / (2 * a)
x2 = (-b + math.sqrt(delta)) / (2 * a)
# print(f"方程有两个解,x1={x1}, x2={x2}")
return x1, x2
点评
本题中规中矩,难度适中,解题思路较为容易想到。不过本题有一定的计算量,计算时需要一些耐心。在计算之前可以先画个草图,并且通过草图其实很容易能够猜想出线段 $MN$ 的中点坐标。如果能够快速判断,对于本题证明性的计算会更加地有信心。
函数与导数
- 已知函数 $f(x) = (\frac{1}{x}+a)\ln(x+1)$。
(1) 当 $a=-1$ 时,求函数 $f(x)$ 在 $(1,f(1))$ 处的切线方程。
(2) 是否存在实数 $a,b$,使得函数 $y = f(\frac{1}{x})$ 关于直线 $x=b$ 对称?若存在,求出 $a,b$ 的值。
(3) 若函数 $f(x)$ 在 $(0,+\infty)$ 内有极值点,求 $a$ 的取值范围。
解:
(1)
当 $a=-1$ 时,
$$ f(x) = (\frac{1}{x}-1)\ln(x+1) $$对其求一阶导数,得到
$$ f'(x) = -\frac{1}{x^2}\ln(x+1)+\frac{1}{x+1}(\frac{1}{x}-1) $$可以计算出点 $(1,f(1))$ 的斜率 $f’(1)=-\ln2$。又 $f(1)=0$,故可以用点斜式写出切线方程
$$ y = (-\ln2)(x-1) $$(2)
令 $g(x)=f(\frac{1}{x})$,可以得到
$$ g(x) = (x+a)\ln(\frac{1}{x}+1) $$其中
$$ \begin{cases} x \ne 0 \\ \frac{1}{x}+1 > 0 \end{cases} $$可以解得 $g(x)$ 的定义域为 $(-\infty,-1) \cup (0,+\infty)$。
由题意可知,$g(x)$ 关于直线 $x=b$ 对称,等价于
$$ g(b+x) = g(b-x) $$对于 $\forall x \in (-\infty,-1)\cup(0,+\infty)$ 恒成立,即
$$ (b+x+a)\ln(\frac{1}{b+x}+1) = (b-x+a)\ln(\frac{1}{b-x}+1) $$对于恒成立的等式,参数的取值通常能够使变量 $x$ 前的系数为零或者能够让含变量 $x$ 的式子约分,最终使得等式不含变量 $x$。
然而,这个式子含有对数函数,不便于化简为参数和变量的线性运算的形式。而我们知道对数函数经过一次求导可以变成有理的幂函数,因此我们尝试求解 $g(x)$ 的一阶导数
$$ g'(x) = \ln(\frac{1}{x}+1) - \frac{x+a}{x(x+1)} $$由于原函数中的对数函数前有一个一次函数作为乘积,求一阶导数仍然存在常数倍的对数函数,所以继续求解 $g(x)$ 的二阶导数
$$ \begin{aligned} g''(x) &= -\frac{1}{x(x+1)} - \frac{x(x+1)-(2x+1)(x+a)}{x^2(x+1)^2} \\ &= \frac{(2x+1)(x+a)-2x(x+1)}{x^2(x+1)^2} \\ &= \frac{(2a-1)x+a}{x^2(x+1)^2} \end{aligned} $$可以看到,二阶导数已经没有对数函数了,完全化为有理函数。
同样,通过求导运算,我们可以得出如下推论:对 $\forall x \in (-\infty,-1)\cup(0,+\infty)$
$$ \begin{aligned} & g(b+x) = g(b-x) \\ \Longleftrightarrow \quad & g'(b+x) = -g'(b-x) \\ \Longleftrightarrow \quad & g''(b+x) = g''(b-x) \end{aligned} $$事实上,根据求导和积分互逆运算的基本性质,这里完全可以划等价符号。
此时,我们再将二阶导数相等的等式列出来
$$ \frac{(2a-1)(b+x)+a}{(b+x)^2(b+x+1)^2} = \frac{(2a-1)(b-x)+a}{(b-x)^2(b-x+1)^2} $$我们稍稍对分子分母按 $x$ 进行整理,得到
$$ \begin{aligned} & \frac{(2a-1)x+2ab+a-b}{(x^2+2bx+b^2)[x^2+2(b+1)x+(b+1)^2]} \\ =& \frac{(1-2a)x+2ab+a-b}{(x^2-2bx+b^2)[x^2-2(b+1)x+(b+1)^2]} \end{aligned} $$可以看到式子虽然有些复杂,但是有很多项的系数其实很相似,最后可以消去不少项。
而我们的目标是,要解出 $a,b$ 的值,让上面的等式与 $x$ 无关。也就是说,我们最终应当让这个等式所有含 $x$ 的项前的系数为 $0$。
等式两边交叉相乘,得到
$$ \begin{aligned} & [(2a-1)x+(2ab+a-b)](x^2-2bx+b^2)[x^2-2(b+1)x+(b+1)^2] \\ =& [(1-2a)x+(2ab+a-b)](x^2+2bx+b^2)[x^2+2(b+1)x+(b+1)^2] \end{aligned} $$观察上述等式,我们可以看出,这个等式是一个关于 $x$ 的一元五次方程,即
$$ Ax^5+Bx^4+Cx^3+Dx^2+Ex+F=0 $$而且
$$ A=B=C=D=E=F=0 $$我们计算五次项前的系数
$$ A = 2(2a-1) $$令 $A=0$,很容易就可以得到
$$ a = \frac{1}{2} $$这很显然是恒成立的一个必要条件。然后我们将 $a$ 的值代入回原等式化简,得到
$$ \begin{aligned} (x^2-2bx+b^2)[x^2-2(b+1)x+(b+1)^2] \\ =(x^2+2bx+b^2)[x^2+2(b+1)x+(b+1)^2] \end{aligned} $$观察发现,计算三次项前的系数或者一次项前的系数就可以得到关于 $b$ 的式子。这里我们计算三次项前的系数
$$ C = 4b + 4(b+1) $$令 $C=0$,同样也很容易得到
$$ b = -\frac{1}{2} $$故存在实数 $a=\frac{1}{2},b=-\frac{1}{2}$,使得函数 $y = f(\frac{1}{x})$ 关于直线 $x=b$ 对称。
简便解法
由题意可知,$g(x)$ 关于直线 $x=b$ 对称,其中的一个必要条件是定义域关于点 $(b,0)$ 对称。利用这一点,就可以很快判断出
$$ b = -\frac{1}{2} $$这样,题目中所给的对称的条件就可以这样使用
$$ g(x) = g(-1-x) $$即
$$ \begin{aligned} (x+a)\ln(\frac{1}{x}+1) &= (-1-x+a)\ln(\frac{1}{-1-x}+1) \\ (x+a)\ln(\frac{x+1}{x}) &= (-1-x+a)\ln(\frac{x}{x+1}) \end{aligned} $$这里等式两边的对数内的真数互为倒数,那么对数就互为相反数。于是,我们可以继续化简
$$ \begin{aligned} x+a &= x+1-a \\ a &= \frac{1}{2} \end{aligned} $$这样求出 $a,b$ 的值会更加快,节省了不少的计算量。不过这样做需要在最后简单验证一下 $a,b$ 的取值满足对称性的条件,因为一开始我们计算 $b$ 的值的时候逻辑上并不是等价的。
(3)
通常来说,求解满足某种条件时参数的取值范围,一般有如下两大思路:
- 判断单调区间,分类讨论
- 参变分离,转化为恒成立或最值问题
由题意可知,函数 $f(x)$ 在 $(0,+\infty)$ 内有极值点,等价于函数 $f’(x)$ 在 $(0,+\infty)$ 上有零点。我们首先求解 $f(x)$ 的一阶导数
$$ f'(x) = -\frac{1}{x^2}\ln(x+1)+\frac{1}{x+1}(\frac{1}{x}+a) $$下面,我们分别采用上述两种思路解答这个问题。
分类讨论
观察 $f(x)$ 一阶导数的解析式,我们发现对数函数前面有分式。对于这种情况,必须要把分母作为公因式提到括号外面,这样括号里面的式子求导之后就不会再出现对数函数了。因此,我们对 $f’(x)$ 作如下变形
$$ f'(x) = \frac{1}{x^2}[\frac{ax^2+x}{x+1}-\ln(x+1)] $$然后我们令
$$ \varphi(x) = \frac{ax^2+x}{x+1}-\ln(x+1) $$对 $\varphi(x)$ 求一阶导数
$$ \begin{aligned} \varphi'(x) &= \frac{(2ax+1)(x+1)-ax^2-x}{(x+1)^2} - \frac{1}{x+1} \\ &= \frac{x(ax+2a-1)}{(x+1)^2} \end{aligned} $$考虑到 $f(x)$ 的定义域为 $x \in (0,+\infty)$,因此 $ax+2a-1$ 的正负就决定了 $\varphi’(x)$ 的正负,也就决定了 $\varphi(x)$ 的单调性。于是,我们令 $ax+2a-1=0$,用 $x$ 表示 $a$,得到
$$ a = \frac{1}{x+2} \in (0,\frac{1}{2}) $$所以,我们应该分如下三种情况讨论。
- $a \leqslant 0$
这时 $ax+2a-1 \leqslant 0$,$\varphi’(x) \leqslant 0$,$\varphi(x)$ 单调递减。
又 $\varphi(0)=0$,所以对于 $\forall x \in (0,+\infty)$,$\varphi(x)<0$。也就是 $f’(x)<0$ 在 $(0,+\infty)$ 上恒成立。
那么,$f(x)$ 在 $(0,+\infty)$ 上单调递减,不可能存在极值点。
- $a \geqslant \frac{1}{2}$
这时 $ax+2a-1 \geqslant 0$,$\varphi’(x) \geqslant 0$,$\varphi(x)$ 单调递增。
又 $\varphi(0)=0$,所以对于 $\forall x \in (0,+\infty)$,$\varphi(x)>0$。也就是 $f’(x)>0$ 在 $(0,+\infty)$ 上恒成立。
那么,$f(x)$ 在 $(0,+\infty)$ 上单调递增,同样也不可能存在极值点。
- $0<a<\frac{1}{2}$
这时 $\varphi(x)$ 的导函数 $\varphi’(x)$ 存在零点
$$ x = \frac{1-2a}{a} $$函数 $\varphi(x)$ 导函数的正负以及原函数的单调性如下表:
| 区间 | $\varphi’(x)$ 的正负 | $\varphi(x)$ 的单调性 |
|---|---|---|
| $(0,\frac{1-2a}{a})$ | $-$ | $\searrow$ |
| $(\frac{1-2a}{a},+\infty)$ | $+$ | $\nearrow$ |
又 $\varphi(0)=0$,所以 $\varphi(\frac{1-2a}{a})<0$。而 $\lim_{x \rightarrow +\infty} \varphi(x)>0$,由零点存在性定理可知
$$ \exists x \in (\frac{1-2a}{a},+\infty), \quad \textrm{s.t.} \quad \varphi(x)=0 $$记这个零点 $x=\alpha$。于是函数 $\varphi(x)$ 的正负,函数 $f(x)$ 导函数的正负以及原函数的单调性如下表:
| 区间 | $\varphi(x)$ 的正负 | $f’(x)$ 的正负 | $f(x)$ 的单调性 |
|---|---|---|---|
| $(0,\alpha)$ | $-$ | $-$ | $\searrow$ |
| $(\alpha,+\infty)$ | $+$ | $+$ | $\nearrow$ |
这充分说明了 $f(x)$ 有一个极值点 $x=\alpha$。
综上所述,$a$ 的取值范围是 $(0,\frac{1}{2})$。
可视化
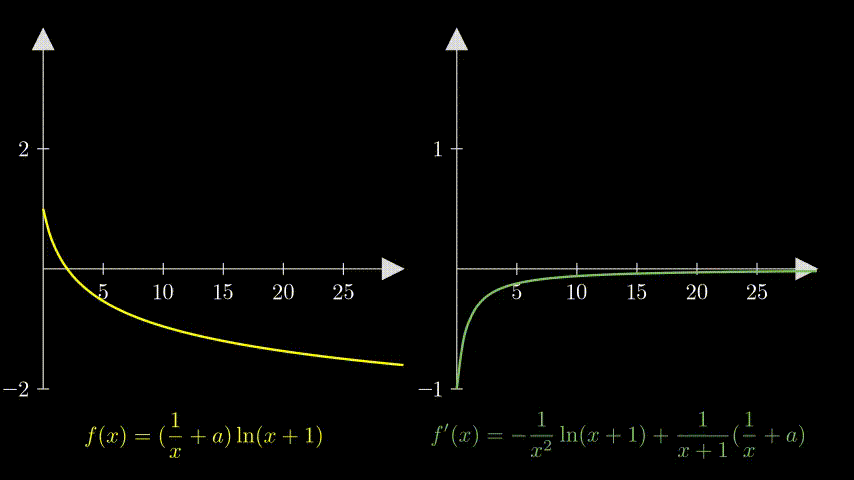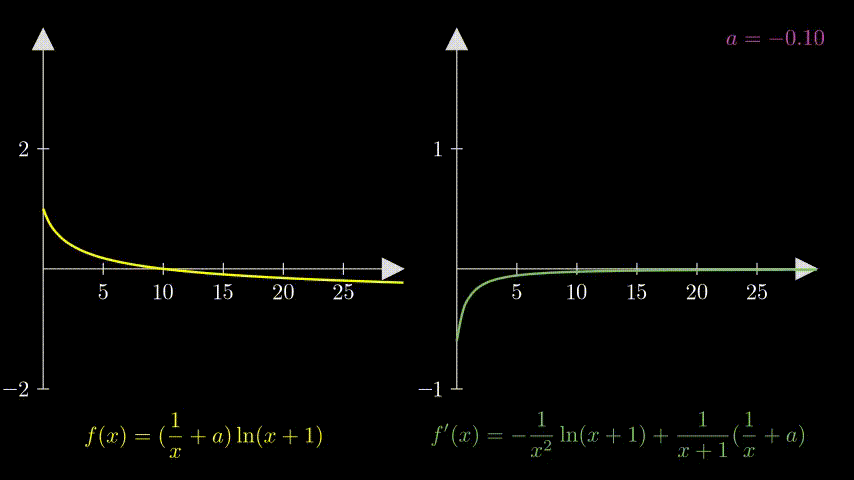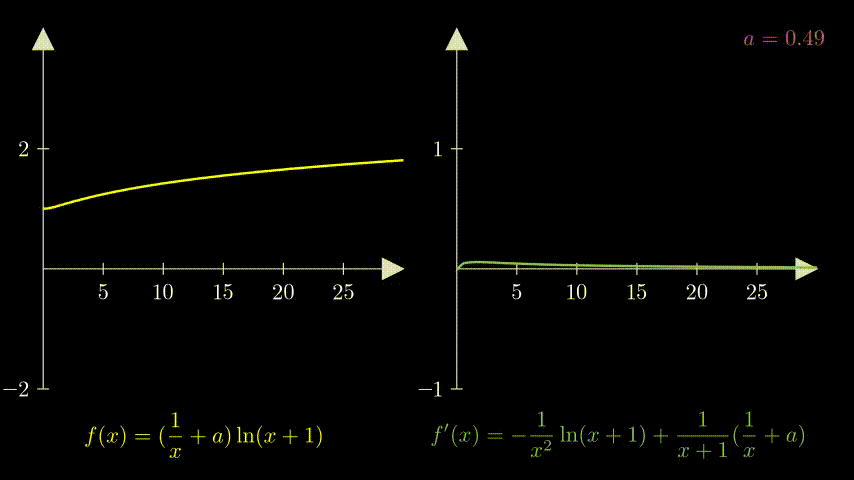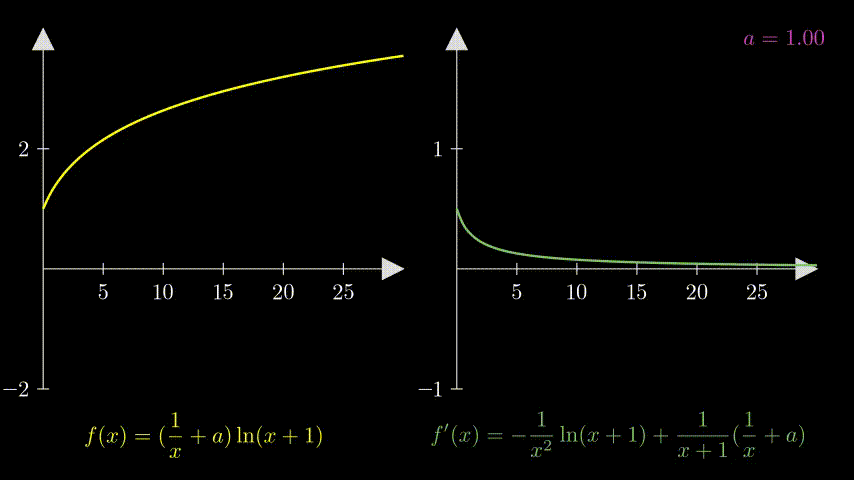
from manim import *
class MyFunction(Scene):
def __init__(self):
super().__init__()
self.a = ValueTracker(-0.5)
self.fx_axes = Axes(
x_range=[0, 30, 5],
y_range=[-2, 4, 2],
x_length=6,
y_length=6,
axis_config={"stroke_color": GREY_A, "stroke_width": 2},
)
self.fx_axes.add_coordinates()
self.grad_fx_axes = Axes(
x_range=[0, 30, 5],
y_range=[-1, 2, 1],
x_length=6,
y_length=6,
axis_config={"stroke_color": GREY_A, "stroke_width": 2},
)
self.grad_fx_axes.add_coordinates()
self.fx_label = MathTex(r"f(x) = (\frac{1}{x}+a) \ln(x+1)")
self.fx_label.set_color(YELLOW).scale(0.75)
self.grad_fx_label = MathTex(r"f'(x) = -\frac{1}{x^2}\ln(x+1)+\frac{1}{x+1}(\frac{1}{x}+a)")
self.grad_fx_label.set_color(GREEN).scale(0.75)
self.group = Group(self.fx_axes, self.grad_fx_axes, self.fx_label, self.grad_fx_label).arrange_in_grid()
self.fx_graph = always_redraw(self.get_fx)
self.grad_fx_graph = always_redraw(self.get_grad_fx)
self.a_label = MathTex(r"a = %.2f" % self.a.get_value()).set_color(PINK).scale(0.75).to_corner(UR)
self.a_label.add_updater(
lambda x: x.become(MathTex(r"a = %.2f" % self.a.get_value()).set_color(PINK).scale(0.75).to_corner(UR)))
def construct(self):
self.add(self.fx_axes, self.fx_label, self.grad_fx_axes, self.grad_fx_label)
self.add(self.fx_graph, self.grad_fx_graph)
self.wait()
self.play(Create(self.a_label))
self.wait()
self.play(self.a.animate.set_value(0), run_time=5)
self.wait()
self.play(self.a.animate.set_value(0.5), run_time=5)
self.wait()
self.play(self.a.animate.set_value(1), run_time=5)
self.wait()
def fx(self, x):
a = self.a.get_value()
if x == 0:
return 1
else:
return (1 / x + a) * np.log(x + 1)
def grad_fx(self, x):
a = self.a.get_value()
if x == 0:
return a - 0.5
else:
return -np.log(x + 1) / np.power(x, 2) + (1 / x + a) / (x + 1)
def get_fx(self):
return self.fx_axes.plot(self.fx, color=YELLOW)
def get_grad_fx(self):
return self.grad_fx_axes.plot(self.grad_fx, color=GREEN)
参变分离
令 $f’(x)=0$,把 $a$ 表示成关于 $x$ 的函数
$$ a = \frac{(x+1)\ln(x+1)}{x^2} - \frac{1}{x} $$将这个关于 $a$ 的函数记作 $h(x)$,即
$$ h(x) = \frac{(x+1)\ln(x+1)-x}{x^2} $$既然 $f’(x)$ 存在零点,那么直线 $y=a$ 与曲线 $y=h(x)$ 应该有交点。于是问题转化为求 $h(x)$ 的值域。我们首先对 $h(x)$ 求一阶导数
$$ \begin{aligned} h'(x) &= \frac{[\ln(x+1)+1-1]x^2-2x[(x+1)\ln(x+1)-x]}{x^4} \\ &= \frac{2x-(x+2)\ln(x+1)}{x^3} \end{aligned} $$一阶导数的正负仍然不好判断,将分子记作 $m(x)$,即
$$ m(x) = 2x-(x+2)\ln(x+1) $$求解 $m(x)$ 的一阶导数
$$ m'(x) = 1-\ln(x+1)-\frac{1}{x+1} $$$m(x)$ 的一阶导数还存在常数倍的对数函数,再求一次导就可以化为有理函数。
$$ \begin{aligned} m''(x) &= -\frac{1}{x+1} + \frac{1}{(x+1)^2} \\ &= -\frac{x}{(x+1)^2} < 0 \end{aligned} $$所以 $m’(x)$ 在 $(0,+\infty)$ 上单调递减
$$ m'(x) < \lim_{x \rightarrow 0^+} m'(x) = 0 $$所以 $m(x)$ 在 $(0,+\infty)$ 上单调递减
$$ m(x) < \lim_{x \rightarrow 0^+} m(x) = 0 $$这样我们很容易地就判断出 $h’(x)$ 的分子恒负,即 $h’(x)<0$,$h(x)$ 在 $(0,+\infty)$ 上单调递减。
那么 $h(x)$ 的最大值应该无限逼近于 $h(0)$。但是 $h(x)$ 在 $x=0$ 处没有定义,所以计算 $x \rightarrow 0^+$ 时 $h(x)$ 的极限,即
$$ \begin{aligned} \lim_{x \rightarrow 0^+} h(x) &= \lim_{x \rightarrow 0^+} \frac{(x+1)\ln(x+1)-x}{x^2} \\ &= \lim_{x \rightarrow 0^+} \frac{(x+1)[x-\frac{1}{2}x^2+o(x^2)]-x}{x^2} \\ &= \lim_{x \rightarrow 0^+} \frac{\frac{1}{2}x^2+x+o(x^2)-x}{x^2} \\ &= \frac{1}{2} \end{aligned} $$在计算上述极限时,将对数函数二阶泰勒展开,是因为对数函数前的多项式函数的最低次数为 $0$(含常数项),而分母的次数为 $2$,因此至少需要展开到二阶。
同理,$h(x)$ 的最小值应该无限逼近 $x \rightarrow +\infty$ 处的极限值,即
$$ \begin{aligned} \lim_{x \rightarrow +\infty} h(x) &= \lim_{x \rightarrow +\infty} \frac{(x+1)\ln(x+1)-x}{x^2} \\ &= \lim_{x \rightarrow +\infty} \frac{\ln(x+1)+1-1}{2x} \\ &= \lim_{x \rightarrow +\infty} \frac{1}{2(x+1)} \\ &= 0 \end{aligned} $$在计算上述极限时,原式是 $\frac{\infty}{\infty}$ 型未定式,使用两次洛必达法则即可。
综合以上,可以得到 $a$ 的取值范围
$$ a \in (0,\frac{1}{2}) $$点评
本题题型较为常规,难度适中,并且有虽然不大但是一定程度上的计算量。要注意在处理对数函数时的技巧,如何在求导的过程中尽可能地化繁为简,便于找到函数的零点进行分类讨论。
本题也可以用参变分离的方法求解。虽然省去了分类讨论的麻烦,但是求导过程有一定的计算量,并且需要一定的高等数学求极限的知识。