从圆锥曲线到二次型

---

圆锥曲线及其方程

椭圆的标准方程

$$ \begin{align*} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \quad (a, b > 0) \end{align*} $$

当 $a = b = r$ 时，这个方程表示圆

$$ \begin{align*} x^2 + y^2 = r^2 \quad (r > 0) \end{align*} $$

双曲线的标准方程

$$ \begin{align*} \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \quad (a, b > 0) \\ \frac{y^2}{a^2} - \frac{x^2}{b^2} = 1 \quad (a, b > 0) \end{align*} $$

抛物线的标准方程

$$ \begin{align*} y^2 = 2px \\ x^2 = 2py \end{align*} $$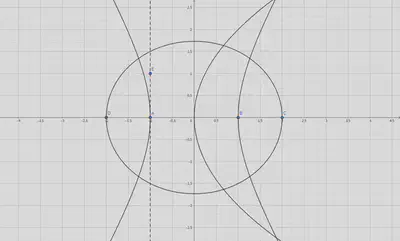

圆锥曲线的一般方程

圆锥曲线的一般方程是一个关于 $x, y$ 的二次方程

$$ \begin{align*} Ax^2 + By^2 + 2Cxy + 2Dx + 2Ex + F = 0 \tag{1} \end{align*} $$

之所以有部分项的前面有系数 $2$，是为了方便用高等代数的形式来表示，即

$$ \begin{align*} \begin{bmatrix} x & y & 1 \end{bmatrix} \begin{bmatrix} A & C & D \\ C & B & E \\ D & E & F \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = 0 \tag{2} \end{align*} $$

圆锥曲线的形状判定

旋转变换矩阵

$$ R = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} $$

它是一个正交矩阵，这意味着

$$ R R^{\top} = R^{\top} R = I $$

又因为逆矩阵的定义

$$ \begin{align*} R R^{-1} = R^{-1} R = I \end{align*} $$

所以

$$ \begin{align*} R^{-1} = R^{\top} \end{align*} $$

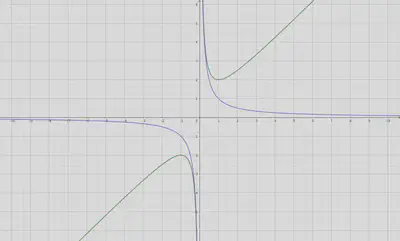
我们所熟知的反比例函数图像为什么是双曲线，是因为

$$ \begin{align*} xy &= k \end{align*} $$

的两条渐近线分别为 $x$ 轴和 $y$ 轴。作变量变换

$$ \begin{align*} \begin{bmatrix} u \\ v \end{bmatrix} &= \begin{bmatrix} \frac{\sqrt{2}}{2} & -\frac{\sqrt{2}}{2} \\ \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \end{align*} $$

反解出

$$ \begin{align*} \begin{bmatrix} x \\ y \end{bmatrix} &= \begin{bmatrix} \frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \\ -\frac{\sqrt{2}}{2} & \frac{\sqrt{2}}{2} \end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix} \end{align*} $$

代入原方程得

$$ \begin{align*} \left(\frac{\sqrt{2}}{2}u + \frac{\sqrt{2}}{2}v \right) \left(-\frac{\sqrt{2}}{2}u + \frac{\sqrt{2}}{2}v\right) &= k \\ v^2 - u^2 &= 2k \\ \frac{v^2}{2k} - \frac{u^2}{2k} &= 1 \end{align*} $$

同样，对勾函数（也称为双勾函数）的图像也是双曲线，是因为

$$ \begin{align*} y = x + \frac{k}{x} \end{align*} $$

的两条渐近线分别为

$$ \begin{align*} x = 0 \\ y = x \end{align*} $$

作变量变换

$$ \begin{align*} \begin{bmatrix} u \\ v \end{bmatrix} &= \begin{bmatrix} \cos \frac{\pi}{8} & -\sin \frac{\pi}{8} \\ \sin \frac{\pi}{8} & \cos \frac{\pi}{8} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} \end{align*} $$

由角平分线第二定理，可以快速计算出 $\frac{\pi}{8}$ 的正弦值为

$$ \begin{align*} \sin \frac{\pi}{8} &= \sin \frac{\pi}{4} \cdot \frac{1}{\sqrt{2} + 1} \\ &= 1 - \frac{\sqrt{2}}{2} \\ \Longrightarrow \cos \frac{\pi}{8} &= \sqrt{1 - \sin^{2} \frac{\pi}{8}} \\ &= \sqrt{\sqrt{2} - \frac{1}{2}} \end{align*} $$

接着，求出旋转变换的逆矩阵即可反解出 $x, y$，代入原式即可证明。

矩阵相似对角化

系数矩阵

$$ P = \begin{bmatrix} A & C & D \\ C & B & E \\ D & E & F \end{bmatrix} $$

是一个实对称矩阵，所以它必定可相似对角化，即存在可逆矩阵 $Q$，使得

$$ \begin{align*} Q^{-1} P Q &= \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} \\ P &\sim \begin{bmatrix} \lambda_1 & & \\ & \lambda_2 & \\ & & \lambda_3 \end{bmatrix} \end{align*} $$

其中，$\lambda_1$, $\lambda_2$, $\lambda_3$ 为特征值。相似的矩阵具有相同的特征值，它刻画了特征向量的伸缩倍数。

注意这里的 $\lambda_1$, $\lambda_2$ 是直接对 $x, y$ 作用的，它们共同影响了圆锥曲线的形状。下面我们就来进行深入分析。

圆锥曲线的不变量

圆锥曲线一共有如下 3 个不变量

$$ \begin{align*} I_1 &= \operatorname{tr} \begin{pmatrix} A & C \\ C & B \end{pmatrix} = A + B \\ I_2 &= \operatorname{det} \begin{pmatrix} A & C \\ C & B \end{pmatrix} = AB - C^2 \\ I_3 &= \operatorname{det} \begin{pmatrix} A & C & D \\ C & B & E \\ D & E & F \end{pmatrix} \end{align*} $$

其中，$I_2$ 是重要的判断圆锥曲线形状的依据。若

$$ \begin{bmatrix} A & C \\ C & B \end{bmatrix} \sim \begin{bmatrix} \lambda_1 & \\ & \lambda_2 \end{bmatrix} $$

作为对角矩阵的特征值，不妨设 $\lambda_1 < \lambda_2$，那么

1. 若 $0 < \lambda_1 < \lambda_2$, 则该圆锥曲线是椭圆。
2. 若 $\lambda_1 < 0 < \lambda_2$, 则该圆锥曲线是双曲线。
3. 若 $0 = \lambda_1 < \lambda_2$，则该圆锥曲线是抛物线。

并且，可以确定椭圆或双曲线的离心率为

$$ e = \sqrt{1 - \frac{\lambda_1}{\lambda_2}} \begin{cases} = 0 \quad \text{圆} \\ \in (0, 1) \quad \text{椭圆} \\ = 1 \quad \text{抛物线} \\ \in (1, +\infty) \quad \text{双曲线} \end{cases} $$

又因为任意方阵 $A$ 的所有特征值之积等于 $A$ 的行列式，即

$$ \prod_{i} \lambda_i = \operatorname{det} A $$

所以

$$ I_2 = AB - C^2 \begin{cases} < 0 \quad \text{双曲线} \\ = 0 \quad \text{抛物线} \\ > 0 \quad \text{椭圆} \end{cases} $$

二次曲面及其方程

从二维升至三维后，情况虽然变得更为复杂，但是总有一些根本的不变量和规律。首先，我们先直观地感受一下二次曲面的种类和分类。

椭球面

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1 \quad (a, b, c > 0) $$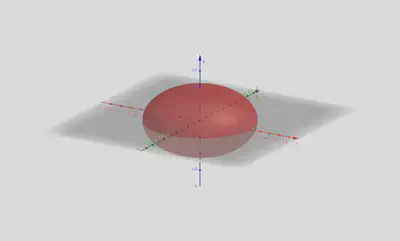

特别地，当 $a = b = c = r$ 时，方程表示球面

$$ x^2 + y^2 + z^2 = r^2 \quad (r > 0) $$

由于双曲线和抛物线不是封闭曲线，所以它们不可能形成类似于球面的封闭曲面。

椭圆锥面

$$ \frac{x^2}{a^2} + \frac{y^2}{b^2} = z^2 \quad (a, b > 0) $$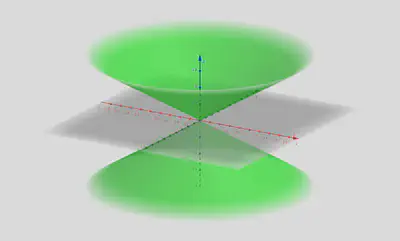

特别地，当 $a = b = r$ 时，方程表示圆锥面

$$ \frac{x^2}{r^2} + \frac{y^2}{r^2} = z^2 \quad (r > 0) $$

二次柱面

圆锥曲线沿某个坐标轴运动的轨迹就形成了二次柱面，即

$$ \begin{align*} \frac{x^2}{a^2} + \frac{y^2}{b^2} &= 1 \quad (a, b > 0) \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} &= 1 \quad (a, b > 0) \\ y^2 &= 2px \end{align*} $$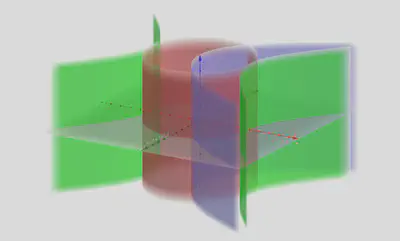

双曲面

双曲线沿其不同的对称轴旋转的轨迹形成了不同的双曲面，包括单叶双曲面和双叶双曲面，即

$$ \begin{align*} \frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2} &= 1 \quad (a, b, c > 0) \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} - \frac{z^2}{c^2} &= 1 \quad (a, b, c > 0) \\ \end{align*} $$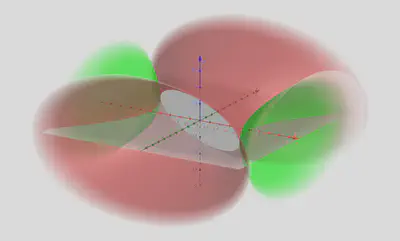

抛物面

椭圆和双曲线的标准方程都是二次齐次式，它们可以在更高的三维空间中和抛物线相结合，形成椭圆抛物面和双曲抛物面（马鞍面）。

$$ \begin{align*} \frac{x^2}{a^2} + \frac{y^2}{b^2} &= z \quad (a, b > 0) \\ \frac{x^2}{a^2} - \frac{y^2}{b^2} &= z \quad (a, b > 0) \end{align*} $$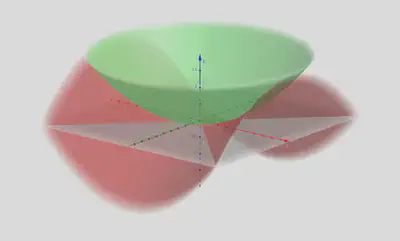

二次曲面的一般方程

通过类比推理，二次曲面的一般方程是一个关于 $x, y, z$ 的二次方程。用高等代数的形式表示就是

$$ \begin{bmatrix} x & y & z & 1 \end{bmatrix} \begin{bmatrix} A & D & E & G \\ D & B & F & H \\ E & F & C & J \\ G & H & J & K \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = 0 $$

同理，二次齐次式的系数矩阵

$$ \begin{bmatrix} A & D & E \\ D & B & F \\ E & F & C \end{bmatrix} $$

是判断二次曲面类型的关键。当维度升高后，有必要引入一套更加规范化的理论，这就是二次型。

二次型

$$ \begin{align*} f(x_1, x_2, \cdots, x_n) &= \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix} \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \\ &= x^{\top} A x \end{align*} $$

通过二次型的定义，可以将 $n$ 维空间的任意一个超二次曲面的方程和一个 $n$ 阶对称矩阵对应起来。

矩阵合同

两个矩阵 $A, B$ 合同，即

$$ \begin{align*} A \simeq B \end{align*} $$

等价于，存在一个可逆矩阵 $Q$，使得

$$ \begin{align*} Q^{\top} A Q &= B \end{align*} $$

二次型在可逆变换前后，矩阵合同。又因为二次型和实对称矩阵一一对应，所以任何二次型的系数矩阵一定和一个对角矩阵合同。

标准形

只含平方项的二次型被称为二次型的标准形，即

$$ \begin{align*} f(x_1, x_2, \cdots, x_n) &= \begin{bmatrix} x_1 & x_2 & \cdots & x_n \end{bmatrix} \begin{bmatrix} \lambda_1 & & & \\ & \lambda_2 & & \\ & & \ddots & \\ & & & \lambda_n \end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \\ &= \lambda_1 x_1^2 + \lambda_2 x_2^2 + \cdots + \lambda_n x_n^2 \end{align*} $$

任何二次型都可以通过正交变换化为标准形。具体步骤如下：

1. 求特征值和特征向量
2. 确定齐次线性方程的基础解系
3. 施密特正交化、单位化，得到正交变换矩阵

我们再回到二维平面中，定义二次型

$$ f(x, y) = ax^2 + by^2 = k \quad (k > 0) $$

• 若 $a > 0, b > 0$，二次型表示椭圆。
• 若 $ab < 0$，二次型表示双曲线。

由于抛物线的方程不是二次齐次式，按上述定义无法通过二次型表示抛物线。参考前文的内容，不难发现，一般的二次多项式若表示抛物线，须满足

$$ \begin{align*} I_2 &= \operatorname{det} \begin{pmatrix} A & C \\ C & B \end{pmatrix} = AB - C^2 = 0 \\ I_3 &= \operatorname{det} \begin{pmatrix} A & C & D \\ C & B & E \\ D & E & F \end{pmatrix} \ne 0 \end{align*} $$

类似地，在三维空间中，定义二次型

$$ f(x, y, z) = ax^2 + by^2 + cz^2 = k \quad (k \geqslant 0) $$

• 若 $a, b, c$ 都大于 $0$，二次型表示椭球面。
• 若 $a, b, c$ 有且仅有一个小于 $0$，二次型表示单叶双曲面。
• 若 $a, b, c$ 有且仅有两个小于 $0$，二次型表示双叶双曲面。
• 若 $abc = 0$，二次型是一个柱面。
• 若 $a, b, c$ 不都同号，且 $k = 0$，二次型表示椭圆锥面。

同样地，上述二次齐次式无法表示抛物面。可以用类似二维平面的方法，通过二次曲面的不变量来判断。

规范形和惯性指数

通过上述分析，我们发现二次型的标准形的正负是一个重要指标。通过可逆变换（不能是正交变换），可以把二次型化为规范形。

二次型的规范形经过伸缩变换，特征值发生了变化，且取值范围只能是 $\{1, -1, 0\}$。大于 $0$ 的特征值个数称为正惯性指数，小于 $0$ 的特征值个数称为负惯性指数。

正定二次型

如果一个二次型的特征值都大于 $0$，即正惯性指数 $p = n$，那么该二次型就是一个正定二次型。显然，椭圆、椭球面都是正定二次型，双曲线、双曲面都是不定二次型。

不难发现，不论是二维平面的椭圆，还是三维空间的椭球面，它们具有一个共同的特点：封闭。这意味着，如果一个多元函数是正定的，那么它必然存在最优解。这在凸优化等领域得到广泛应用。