图解 Flash Attention
Flash Attention 是目前针对 Attention 计算最优解决方案的开山工作,旨在从底层 GPU 的 HBM(High Bandwidth Memory)和 GPU 的片内 SRAM(Static Random Access Memory)的角度尽可能降低访存开销,从而加速 Attention 的计算,在长序列的情况下展现出了优良的性能。
然而,Flash Attention 对于 LLM 初学者来说很不好理解,因为它需要我们对 Attention 的计算过程有非常深入的了解,而其中的难点在于 Softmax 的计算的可分割性的理解。本文希望通过丰富的插图乃至动画,让 Flash Attention 能够通俗易懂。
概述
Flash Attetention 的研究动机是降低 Attention 计算过程中 GPU 的 HBM 和片内 SRAM 之间的访存开销。对此,Flash Attention 主要应用了如下两个技术:
- Tiling:将输入划分为多个块,通过循环遍历每个块,在每个块上执行精简化的 Softmax 计算;
- Recompute:存储来自前向传播的 softmax 归一化因子,而不从 HBM 读写注意力矩阵。
于是,每次循环迭代的过程中,自注意力计算就被 fuse 到了一个 GPU kernel 中,从而实现了对 GPU 内存的更细粒度的控制和优化。
架构
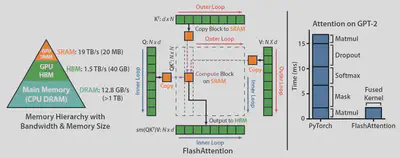
左图显示了 GPU 的三级存储结构,从上到下分别是 SRAM、HBM 和 CPU Main Memory。由计算机体系结构的基本常识可知,从上到下的访存速度越来越慢,而存储容量越来越大,离计算单元越来越远。
中间的图即为 Flash Attention 的框架流程图。整个图的结构应该从外到内看:周围的四个部分分别是 Attention 的 3 个输入 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$ 和输出 $\mathbf{O}$,它们是存储在 HBM 中的;中间虚线内的部分即为 SRAM,它是直接负责和计算单元进行交互的。整个计算过程是一个二重循环,外循环是对 $\mathbf{K}$ 和 $\mathbf{V}$,而内循环是对 $\mathbf{Q}$ 和 $\mathbf{O}$ 的。
右图则展现了 Flash Attention 的优良性能,将原始的 GPT-2 Attention block 内的算子进行融合,极大地降低了计算和访存的时延。
算法原理
标准 Attention 及其瓶颈

首先我们要知道一点,标准 Attention 的输入和输出都在 HBM 中。上图显示了标准 Attention 的计算过程,主要分为以下 3 步:
- 读取 $\mathbf{Q}, \mathbf{K}$,计算一次注意力,将得分 $\mathbf{S}$ 写回内存
- 读取得分,计算 Softmax,将结果 $\mathbf{P}$ 写回内存
- 读取 $\mathbf{V}$,再计算一次注意力,将结果 $\mathbf{O}$ 写回内存
可以看到,整个计算过程一共需要 3 次读写内存。在序列长度较大时,很明显会有一定的性能瓶颈。
为什么标准的 Attention 计算需要那么麻烦?根本原因是因为其中的非线性算子 Softmax。我们知道,计算 Softmax 前,需要已知所有样本的特征——因为需要在每个特征上对样本求和。对于 Attention 而言,则需要完整计算 $\mathbf{Q} \mathbf{K}^{\top}$ 的结果。这使我们产生了一个思维惯性,认为好像如果不这样计算,Softmax 的计算结果就不对了——那么我们也就很容易让计算机串行计算整个过程了。后文将深入阐述这个问题及其巧妙的解决方案。
Flash Attention

上图显示了 Flash Attention 的计算过程,看起来似乎很难理解。为了方便说明,更加直观通俗易懂,我们将整个计算过程分为分割(split)和计算两个过程。其中,分割过程首次阅读定然不好理解,因为我们不知其所以然。所以,我们首先来看计算的过程,也就是第 5 行到第 15 行的二重循环。
- 外循环(循环变量
j)- 将 $\mathbf{K}_j, \mathbf{V}_j$ 读入 SRAM
- 内循环(循环变量
i)- 计算得分 $\mathbf{S}_{ij} = \mathbf{Q}_i \mathbf{K}_j^{\top}$
- 计算当前得分 $\mathbf{S}$ 的 Softmax
- 最大值 $\tilde{m}_{ij} = \operatorname{rowmax} (\mathbf{S}_{ij})$
- 取指数 $\tilde{\mathbf{P} }_{ij} = \exp (\mathbf{S}_{ij} - \tilde{m}_{ij})$
- 求和 $\tilde{l}_{ij} = \operatorname{rowsum} (\tilde{\mathbf{P} }_{ij})$
- 计算全局 Softmax
- 更新全局最大值 $m_{i}^{\mathrm{new} } = \max (m_{i}, \tilde{m}_{ij})$
- 更新全局和 $\ell_{i}^{\mathrm{new} } = e^{m_{i} - m_{i}^{\mathrm{new} } } \ell_{i} + e^{\tilde{m}_{ij} - m_{i}^{\mathrm{new} } } \tilde{l}_{ij}$
- 累和修正
- 之前计算的 Softmax 值需要乘以 $\ell_i/\ell_{i}^{\mathrm{new}}$
- 还要再加上 $\dfrac{e^{\tilde{m}_{i j}-m_{i}^{\mathrm {new}}}}{\ell_{i}^{\mathrm {new}}}$ 倍的 $\tilde{\mathbf{P}}_{ij} \mathbf{V}_{j}$
下面的动画演示了整个循环计算的过程:
动画中的计算过程是一个示例,Softmax 计算被分成了 12 块。此时我们再回头看算法的分割阶段,不难理解,$B_c, B_r$ 分别决定了 $\mathbf{Q}, \mathbf{K}, \mathbf{V}, \mathbf{O}$ 的存储空间大小。$T_c, T_r$ 分别表示分块的数量,在这个示例中,$T_c = T_r = 12$。
Softmax Tiling
标准 Softmax 及其瓶颈
对于一组样本 $X = \lbrace x_1, x_2, \ldots, x_n \rbrace$,Softmax 的计算过程如下:
$$ \begin{align*} \operatorname{softmax}(x_i) = \frac{e^{x_i}}{\displaystyle\sum_{j=1}^{n} e^{x_j}} \end{align*} $$不过这种计算方式可能会导致溢出——因为如果数值过大,会造成指数函数的函数值溢出。为了解决这个问题,通常采用最大值归一化的技巧保证数值稳定性。
$$ \begin{align*} \tilde{m} &= \max_{i}{\lbrace x_i \rbrace} \\ \operatorname{softmax}(x_i) &= \frac{e^{x_i - \tilde{m}}}{\displaystyle\sum_{j=1}^{n} e^{x_j - \tilde{m}}} \end{align*} $$下图展示了标准 Softmax 的计算过程:
作为典型的非线性算子,Softmax 的计算需要经历取最大值、取指数和加权平均三个阶段。如若串行计算,则每一步的计算都需要一次读写。
分块计算 Softmax 的理论基础
Softmax 的计算过程中需要取最大值和求和,这需要全局样本的特征信息。是否可以采用分治思想,尝试将计算分块,最后合并这些结果?
下面我们假设一个具有 4 个样本的总体 $X = \lbrace x_1, x_2, x_3, x_4 \rbrace$。我们希望分块计算这 4 个样本的 Softmax,我们进行如下的分块:
$$ \begin{align*} \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \end{bmatrix} = \begin{bmatrix} x^{(1)} \\ x^{(2)} \end{bmatrix} \end{align*} $$其中
$$ \begin{align*} x^{(1)} = \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} \quad x^{(2)} = \begin{bmatrix} x_3 \\ x_4 \end{bmatrix} \end{align*} $$下面的几张图显示了在这种分块方式下计算 Softmax 的过程。
我们希望读者首先要了解一个根本的规律:分块计算是一种对直接计算的抽象。在分块计算的过程中,块内要计算,块间也要相应地计算。前者可并行计算,互不影响;后者不可并行计算,且相互依赖彼此的计算结果。下面的计算过程将处处体现这一根本规律。
计算的第一步,是每个样本都减去最大值。这个过程其实分为分为 3 步:
- 块内求最大值。对应图中第 2 列,其中黄色小圆表示 $x^{(1)}$ 的最大值,红色小圆表示 $x^{(2)}$ 的最大值。
- 块间再求最大值。对应图中第 3 列,其中红色小圆即为总体 $X$ 的最大值。
- 分别都减去最大值。对应图中第 4 列。
同理,取指数的过程也是分为块内和块间共 2 步:
- 块内取指数。对应图中第 2 列。
- 块间再取指数。对应图中第 3 列。
求和的过程其实也分为 2 步:
- 块内求和。对应图中第 2 列。
- 块间再求和。对应图中第 3 列。
不过每个块最终得到的结果是相同的。
最后再取一次加权平均。
在 Flash Attention 中的应用
Flash Attention 中计算 Softmax 并不完全是按照上述过程进行的,但是以此为基础,每次循环通过递推公式进行更新。
实际上,涉及到块间的计算仅取最大值和求和两部分。所以,需要额外的存储空间,并且在每次循环迭代中更新之。
我们反观 Flash Attention 的遍历规则,可以得知外循环是遍历 $\mathbf{K}$ 和 $\mathbf{V}$ 的,内循环是遍历 $\mathbf{Q}$ 和 $\mathbf{O}$ 的。并且,都是在序列长度 $N$ 上进行遍历的。这充分说明了,Flash Attention 将长序列的计算进行了更细粒度的划分。
不过,每次循环遍历时,仅仅只是计算部分 Attention。要向通过部分 Attention 的计算结果,递推出后续的计算结果,直至完整序列的计算结果,对于线性算子 $\mathbf{Q} \mathbf{K}^{\top}$ 和 $\mathbf{P} \mathbf{V}$ 来说较为容易,但对于非线性算子 Softmax 来说较为复杂。
其理论依据恰好为前文所述。只不过在计算当前块的 Softmax 时,还需要对之前的 Softmax 计算结果进行修正。具体来说,就是论文中算法描述的那样:
- 因为新增了样本,样本最大值与求和结果都可能会变化,所以需要更新之前计算的结果。
- 在更新完之前的计算结果后,再将当前循环迭代轮次的计算结果累加上去。
这里的 $\operatorname{diag}$ 表示将向量转化为对角矩阵。由线性变换的基本知识可知,这是一个伸缩变换,相当于矩阵的每个元素都乘或除以一个相应的系数。
复杂度分析
论文在一开始就指出,Flash Attention 相较于标准 Attention,可以将 HBM 访存开销由 $\Theta(Nd + N^2)$ 降低到 $\Theta(N^2d^2M^{-1})$。其中,$N$ 表示序列长度,$d$ 表示注意力头的数量,而 $M$ 表示 SRAM 的存储容量,其取值范围是 $d \leqslant M \leqslant Nd$。那么,最优情况就是 $\Theta(Nd)$,这意味着 Attention 的访存开销成功降低到线性!
这里的 $M$ 是很有讲究的,它的取值与算法伪代码中的分割阶段有着紧密联系。由前文 Softmax 的相关知识,以及动画演示片段可知,每次循环迭代计算的块内 Softmax 是一部分 token,而不是整个序列。显然,SRAM 的存储容量越大,对访存开销的减少就越有帮助。
不过,Flash Attention 需要 $O(N)$ 的额外的存储开销——存储部分最大值和部分和。